Import Libraries

1
2
3
4
5
6
7
8

import pandas as pd
import seaborn as sns

import scipy as sp
from scipy import stats

import warnings
warnings.filterwarnings("ignore")

교차분석

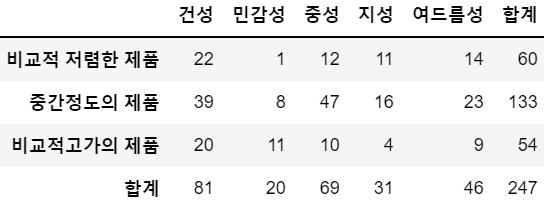
교차표 (Cross-Table)

1
2
3
4

crosstab = pd.crosstab(df.propensity, df.skin, margins=True)

crosstab.columns=[]
crosstab.index=[]
  • margins: 합계(All) 추가 여부
  • normalize: Normalization 여부

cross-table

Chi-square 검정

  • 두 범주형 변수 사이의 관계가 있는지 없는지를 검정 (독립성 검정)
  • 귀무가설: Indepedent (vice versa)
  • 대립가설: Not Independent
1
2
3
4

stats.chisquare(df.column1, df.column2)

# Output
Power_divergenceResult(statistic=291.8166666666667, pvalue=0.023890557260065975)

p-value

  • 관찰 데이터의 검정 통계량이 귀무가설을 지지하는 정도
  • 귀무가설이 참이라는 전제 하에, 관찰이 완료된 값이 표본을 통해 나타날 확률
  • p-value가 0.05(5%) 미만일 경우, 관측치가 나타날 확률이 매우 낮다고 판단하여 귀무가설 기각
  • p-value가 0.05(5%) 이상일 경우, 관측치가 나타날 확률이 충분하다고 판단하여 귀무가설 지지
  • p-value가 0.05 이하라는 것이 항상 대립가설을 의미하는 것은 아님 (5%만큼 귀무가설이 참일 가능성)
1

crosstab.plot.bar(stacked=True)

cross-plot

독립표본 T-test 분석 시각화

  • 서로 다른 집단에서 같은 열 비교
  • 두 집단 간의 평균 차이를 검정
  • ex) “서로 다른” 성별 간에 전반적인 만족도의 평균값 사이에 유의미한 차이가 “없다”
1
2
3
4

stats.ttest_ind(column1.values, column2.values)

# Output
Ttest_indResult(statistic=-0.494589803056421, pvalue=0.6213329051985961)

Box-Plot

boxplot

Histogram

1
2
3
4
5

sns.distplot(male, kde=False, fit=stats.norm,
            hist_kws={'color': 'r', 'alpha': 0.2}, fit_kws={'color': 'r'})

sns.distplot(female, kde=False, fit=stats.norm, 
             hist_kws={'color': 'g', 'alpha': 0.2}, fit_kws={'color': 'g'})

ttest-ind

대응표본 T-test 분석 시각화

  • 동일한 집단에서 서로 다른 열 비교
  • 동일한 모집단으로부터 추출된 두 변수의 평균값을 비교 분석
  • “동일한” 고객 집단이 평가한 구매 가격에 대한
    만족도와 구매 문의에 대한 만족도의 평균값 사이에 유의미한 차이가 있다.
1
2
3
4

stats.ttest_rel(df["satisf_b"], df["satisf_i"])

# Output
Ttest_relResult(statistic=-7.155916401026872, pvalue=9.518854506666398e-12)

Histogram

1
2
3
4
5

sns.distplot(df["satisf_b"], kde=False, fit=stats.norm,
            hist_kws={'color': 'r', 'alpha': 0.2}, fit_kws={'color': 'r'})

sns.distplot(df["satisf_i"], kde=False, fit=stats.norm, 
             hist_kws={'color': 'g', 'alpha': 0.2}, fit_kws={'color': 'g'})

ttest-rel

분산분석 시각화

  • 분산분석(ANalysis Of VAriance, ANOVA)
  • 세 개의 집단에서 적어도 하나의 유의미한 차이가 있는가
  • ex) 3가지 구매 동기에 따른 전반적인 만족도의 평균값 중 적어도 하나는 유의미한 차이가 있다.
1
2
3
4

stats.f_oneway(anova1, anova2, anova3)

# Output
F_onewayResult(statistic=4.732129410493065, pvalue=0.009632034309915485)

Histogram

1
2
3

sns.distplot(anova1, kde=False, fit=sp.stats.norm, hist_kws={'color': 'r', 'alpha': 0.2}, fit_kws={'color': 'r'})
sns.distplot(anova2, kde=False, fit=sp.stats.norm, hist_kws={'color': 'g', 'alpha': 0.2}, fit_kws={'color': 'g'})
sns.distplot(anova3, kde=False, fit=sp.stats.norm, hist_kws={'color': 'b', 'alpha': 0.2}, fit_kws={'color': 'b'})

oneway

상관관계 분석 시각화

  • 연속형 변수열들끼리 비교

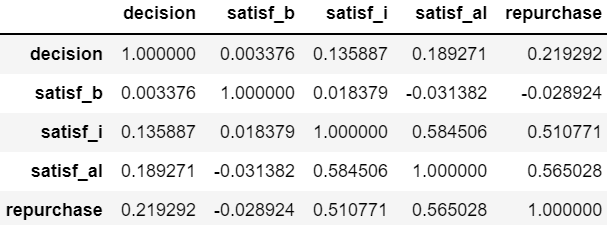
피어슨 상관계수

1

df.corr.corr()
  • -1에 가까울수록 음의 상관관계
  • 1에 가까울수록 양의 상관관계
  • 0에 가까울수록 상관관계가 적음

corr

PairPlot

1

sns.parilpot(df_corr)

pairplot

Iris Data

  • 붓꽃의 품종에 대한 데이터
1
2

iris = sns.load_dataset("iris")
sns.pairplot(iris, kind="reg")
  • reg: 추세선

iris

sepal_width <-> petal_length

  • 두 그룹으로 나눠져 있어 음의 상관관계라 보기 어려움
  • 그룹을 나눠서 비교 (1. 양의 상관관계, 2. 관계 없음)

Simpson’s paradox

simpsons

  • 신장 결석 크기를 치료법 a, b를 사용해서 얼마나 빨리 치료하는지
  • 작은 결석/큰 결석 인원수가 달라서 b 치료법 확률이 낮아짐 > 합계는 높음