[AI SCHOOL 5기] 머신 러닝 실습 - Kernelized SVM
Support Vector Machine #

- 패턴 인식을 위한 지도 학습 모델
- 데이터를 분류하는 Margin을 최대화하는 결정 경계(Decision Boundary)를 찾는 기법
- 결정 경계와 가장 가까운 데이터를 가로지르는 선을 기준으로 Plus & Minus Plane 설정
- Support Vector: 결정 경계와 가장 가까운 데이터의 좌표
- Margin: b11(plus-plane)과 b12(minus-plane) 사이의 거리, 2/w
- 기존의 Hard Margin SVM은 소수의 Noise로 인해 결정 경계를 찾지 못할 수 있음
- Plus & Minus Plane에 약간의 여유 변수를 두어 에러를 무시하는 Soft Margin SVM로 발전
arg min #
$$arg\ min\lbrace\frac{1}{2}{||w||}^2+C\Sigma^n_{i=1}\xi_i\rbrace$$ $$\text{단, }y_i({w}\cdot{x_i}-b)\ge{1-\xi_i},\quad{\xi_i\ge{0}},\quad{\text{for all }1\le{i}\le{n}}$$
- 중괄호 안의 값(w, ξ, b)을 최소화하는 값을 찾는 것
- Margin을 최대화하는 목적 함수(Objective Function)
- Margin(2/w)의 최대화는 w/2의 최소화와 같음 (제곱은 미분 편의성)
- Margin을 침범한 에러(ξ)를 모두 더하고(Σ), Hyper-Parameter인 C를 곱함
- C: 얼마 만큼 여유를 가지고 오류를 허용할 것인지 판단해주는 값
- C가 작을수록 에러를 무시, C가 크면 에러에 민감
Kernel Support Vector Machine #

- 데이터가 선형적으로 분리되지 않을 경우(Lineaerly Unseparable)에 결정 경계를 찾는 기법
- 원본 데이터가 놓여있는 차원을 비선형 매핑을 통해 고차원 공간으로 변환
- Hyper-Parameter인 커널 함수를 컴퓨터가 스스로 찾아내는 것이 Deep Learning
- 커널 함수는 인공신경망의 레이어와 비슷 (Learnable Kernel)
Feature Crosses #
- 데이터를 인공신경망에 밀어넣기 이전에, 기존 열들의 입력값을 조합해서 새로운 데이터 생성
- @ http://j.mp/2p5CbO2
SVC Models #
Linear SVC #
python
from sklearn.svm import LinearSVC
linear_svm = LinearSVC().fit(X, y)Kernelized SVC #
python
from sklearn.svm import SVC
X, y = custom_mglearn.make_handcrafted_dataset()
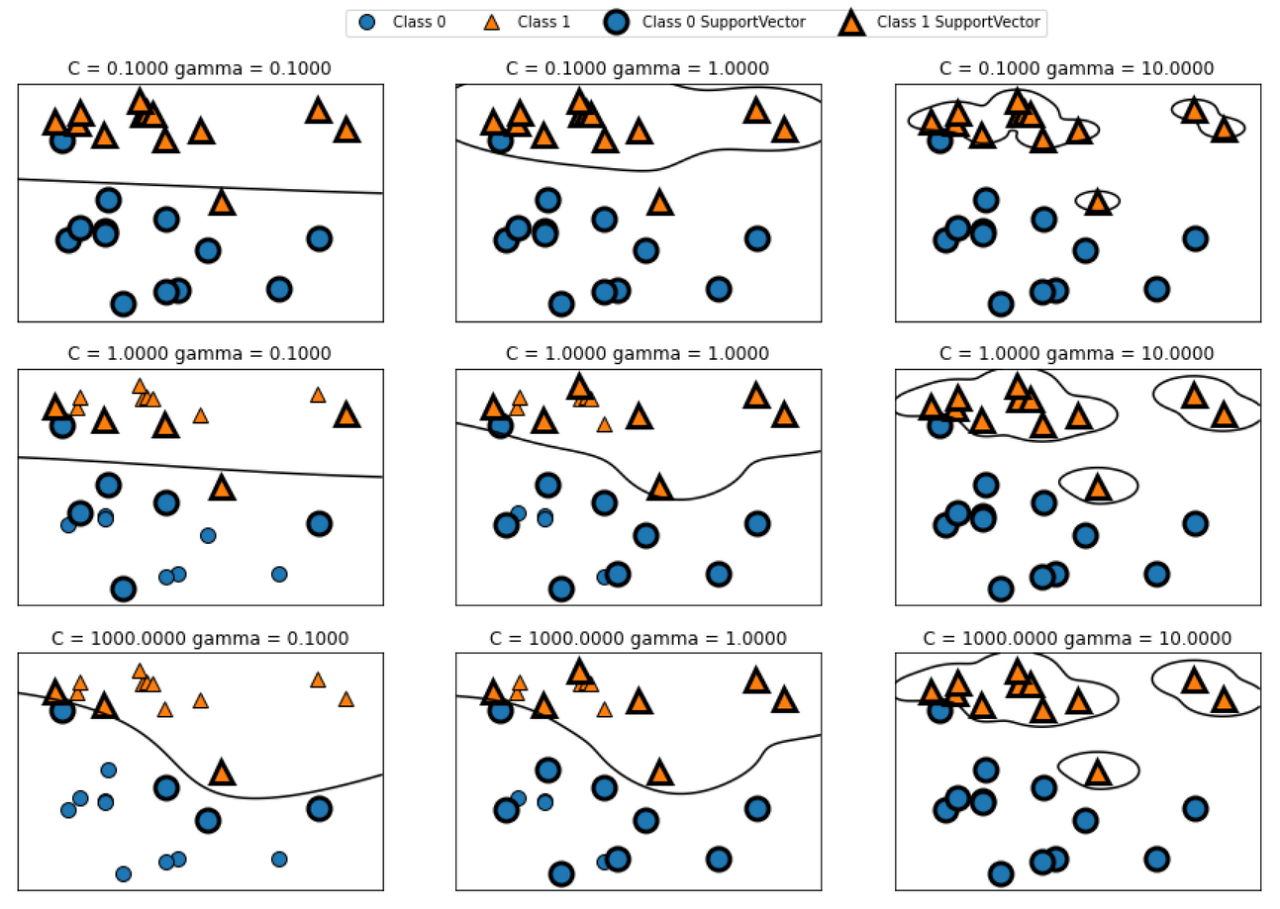
svm = SVC(kernel='rbf', C=10, gamma=0.1).fit(X, y)rbf: 대표적인 커널 함수 (Radial Basis Function, 가우시안 커널 함수)gamma: 가우시안 함수의 단면을 r 이라 할 때, 반지름의 역수(1/r)gamma가 작아질수록 반지름이 커져 선과 같은 형태가 됨
Learning Process #
python
cancer = load_breast_cancer() # 유방암 데이터 (569행, 30열)
X_train, X_test, y_train, y_test = train_test_split(
cancer.data, cancer.target, random_state=0)
svc = SVC(gamma='auto')
svc.fit(X_train, y_train)train_test_split()에test_size가 없으면 기본값 0.25를 Test Data로 지정SVC(gamma='auto'): gamma를 알아서 지정- 분류 모델의 경우,
model.score(X, Y)를 실행하면 Accuracy Score 계산 svc.score(X_train, y_train): Training Data의 Accuracysvc.score(X_test, y_test): Test Data의 Accuracy- 두 데이터의 Accuracy 차이가 심한 것은 열마다 Scale이 달라서 발생하는 문제
- Scaling 후 Hyper-Parameter를 바꿨을 때 두 데이터의 차이가 심하면 Overfitting

Feature Normalization (Scaling) #
- min, max, mean, std를 계산할 때 Training Data만 사용
Min-Max Normalization #
- min(열) = 0, max(열) = 1
- new_X = (old_X - min) / (max - min)
Standardization #
- mean(열) = 0, std(열) = 1
- new_X = (old_X - mean) / std
Scaler Model #
python
sc = StandardScaler() # 또는 MinMaxScaler()
sc.fit(train_X)
train_X_scaled = sc.transform(train_X)
test_X_scaled = sc.transform(test_X)- 새로운 데이터가 들어오면 2차원 행렬 상태로 Scaler를 통과시키고 모델에 입력
- 모델을 저장하고 불러올 때 Scaler도 같이 가져와야 함
- Stanardization이 Min-Max 알고리즘보다 성능이 좋음 (예외 있음)
Grid-Search #
python
from sklearn.model_selection import GridSearchCV
param_grid = {'C' : [0.1, 1, 10, 100, 1000],
'gamma' : [1, 0.1, 0.01, 0.001, 0.0001],
'kernel' : ['rbf']}
grid = GridSearchCV(SVC(), param_grid, refit=True, verbose=1)
grid.fit(X_train_scaled, y_train)- C와 gamma의 후보군을 조합
- 내부적으로 K-Fold로 검증하기 때문에 후보군이 많아질수록 시간이 오래걸림
refit=True: GridSearchCV를 다시 트레이닝 시킴verbose: 값이 커질수록 설명을 상세하게 적어줌GridSearch가 SVC 모델이 되어 Model Fitting, Model Predict 등 과정 진행grid.best_params_: 최적의 C와 gamma의 조합 반환- 내부적으로 검증을 거친 상태이기 때문에 Training Data를 한 번 돌린 것과는 정확도가 다름
Model Tuning (HPO) #
- Grid-Search (Machine Learning)
- Randomized-Search (Deep Learning)
- Bayesian-Search (ML/DL)
Model Predict #
python
from sklearn.metrics import classification_report
grid_predictions = grid.predict(X_test_scaled)
print(classification_report(y_test, grid_predictions))precision: 모델이 양성으로 분류한 것 중 진짜 걸린 것recall: 양성인 것 중 모델이 양성이라 맞춘 것f1-score: Precision과 Recall의 조합support: Test Dataconfusion_matrix도 import해서 사용 가능
| precision | recall | f1-score | support | |
|---|---|---|---|---|
| 0 | 0.98 | 0.94 | 0.96 | 53 |
| 1 | 0.97 | 0.99 | 0.98 | 90 |
| accuracy | 0.97 | 143 | ||
| macro avg | 0.97 | 0.97 | 0.97 | 143 |
| weighted avg | 0.97 | 0.97 | 0.97 | 143 |