1. K-Means Algorithm

  • K는 전체 데이터를 몇 개의 그룹으로 묶어낼 것인지 결정하는 상수
  • 어떤 K 값이 적절한 것인지 파악하는 것이 중요
  • 각각의 데이터마다 중심값까지의 거리를 계속 물어보기 때문에 계산량이 많음
  • 클러스터링 성능을 향상시키기 위해 GPU Accelerated t-SNE for CUDA 활용

Clustering Process

  1. K개의 임의의 중심값을 선택
  2. 각 데이터마다 중심값까지의 거리를 계산하여 가까운 중심값의 클러스터에 할당
  3. 각 클러스터에 속한 데이터들의 평균값으로 각 중심값을 이동
  4. 데이터에 대한 클러스터 할당이 변하지 않을 때까지 2와 3을 반복

2. Learning Process

Model Fitting

1
2
3

from sklearn import cluster

kmeans = cluster.KMeans(n_clusters=2, random_state=0).fit(X)
  • kmeans.labels_: 클러스터 번호
  • kmeans.cluster_centers_: 학습이 끝난 중심값

Model Predict

1

kmeans.predict([[0, 0], [8, 4]]))
  • 각각의 번호가 어떤 클러스터에 속하는지 예측

3. K-Means for Iris Data

Import Libraries

1
2
3
4
5
6
7

import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D

from sklearn import cluster
from sklearn import datasets
from sklearn import metrics
  • Axes3D: 3D 공간에서 시각화하는 함수

Model Fitting

1
2
3

estimators = [('k=8', cluster.KMeans(n_clusters=8)),
              ('k=3', cluster.KMeans(n_clusters=3)),
              ('k=3(r)', cluster.KMeans(n_clusters=3, n_init=1, init='random'))]

Plot Model

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16

fignum = 1
titles = ['8 clusters', '3 clusters', '3 clusters, bad initialization']

for name, est in estimators:
    fig = plt.figure(fignum, figsize=(7, 7))
    ax = Axes3D(fig, elev=48, azim=134)
    est.fit(X)
    labels = est.labels_

    ax.scatter(X[:, 3], X[:, 0], X[:, 2], c=labels.astype(np.float), edgecolor='w', s=100)

    ...
    
    fignum = fignum + 1

plt.show()
  • plt.figure(fignum): plot을 여러 개 생성 (subplot()은 하나의 plot을 분리)
  • Axes3D(elev, azim): elevation (축의 고도), azimuth (방위각)
  • astype: 색깔 칠해주는 옵션
  • edgecolor: 테두리
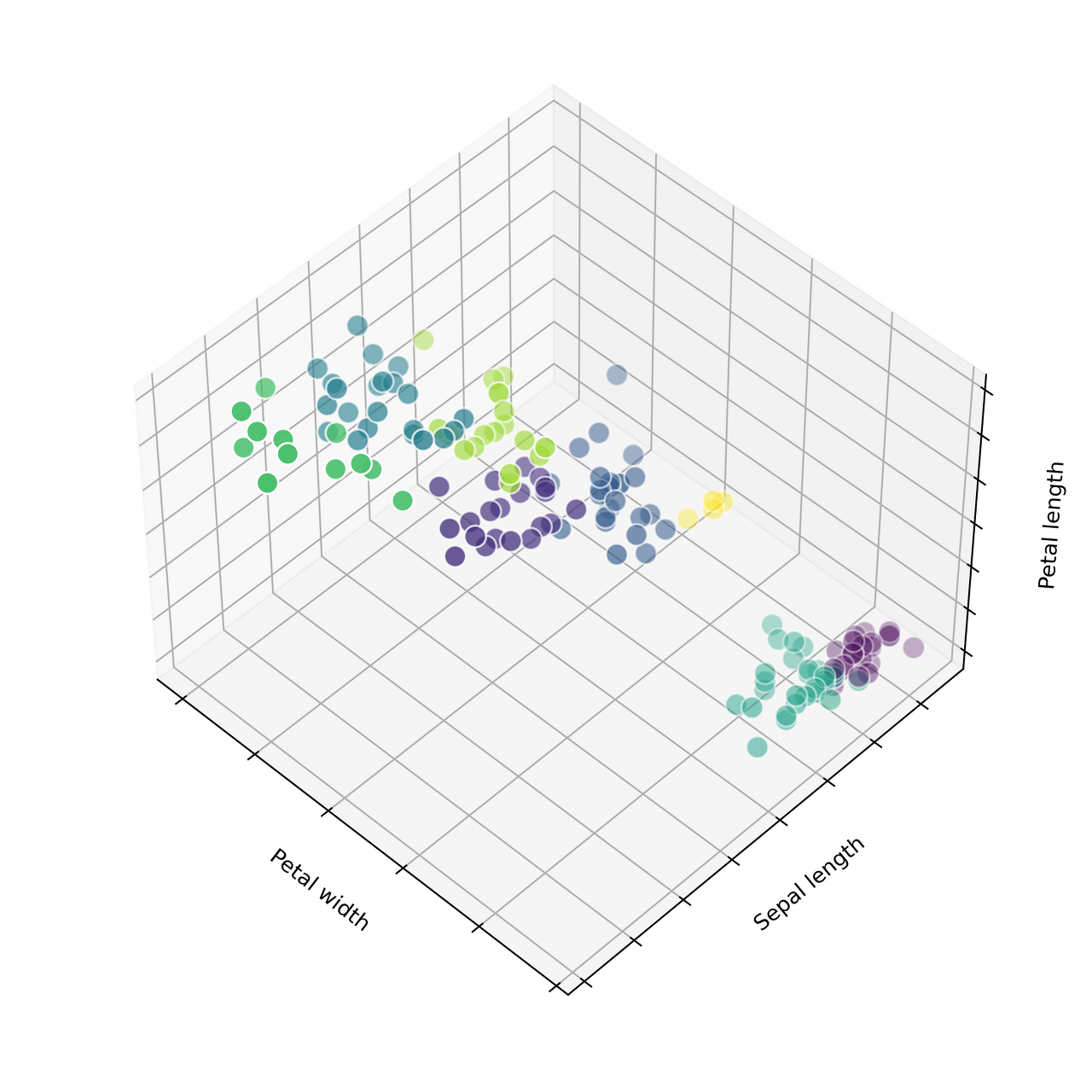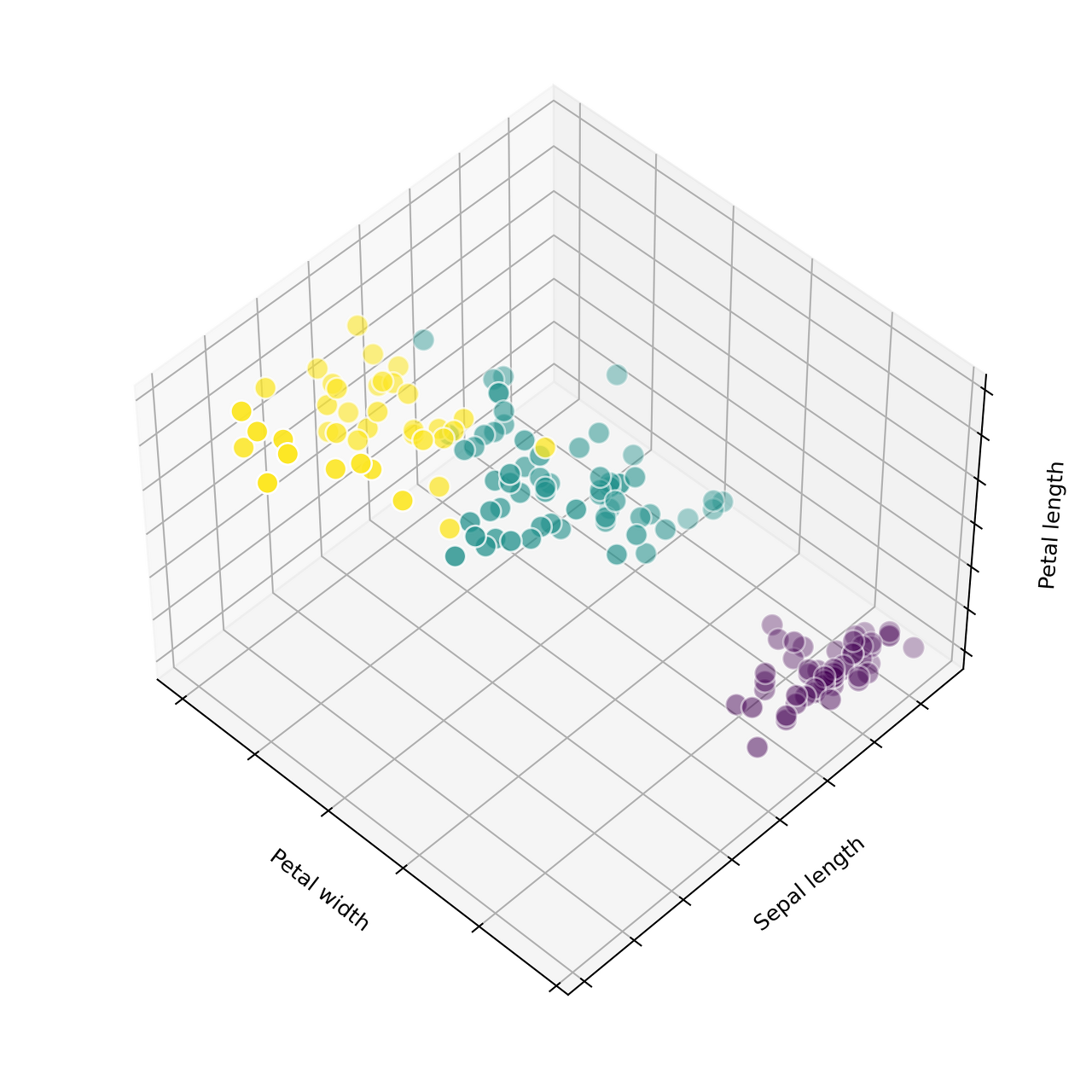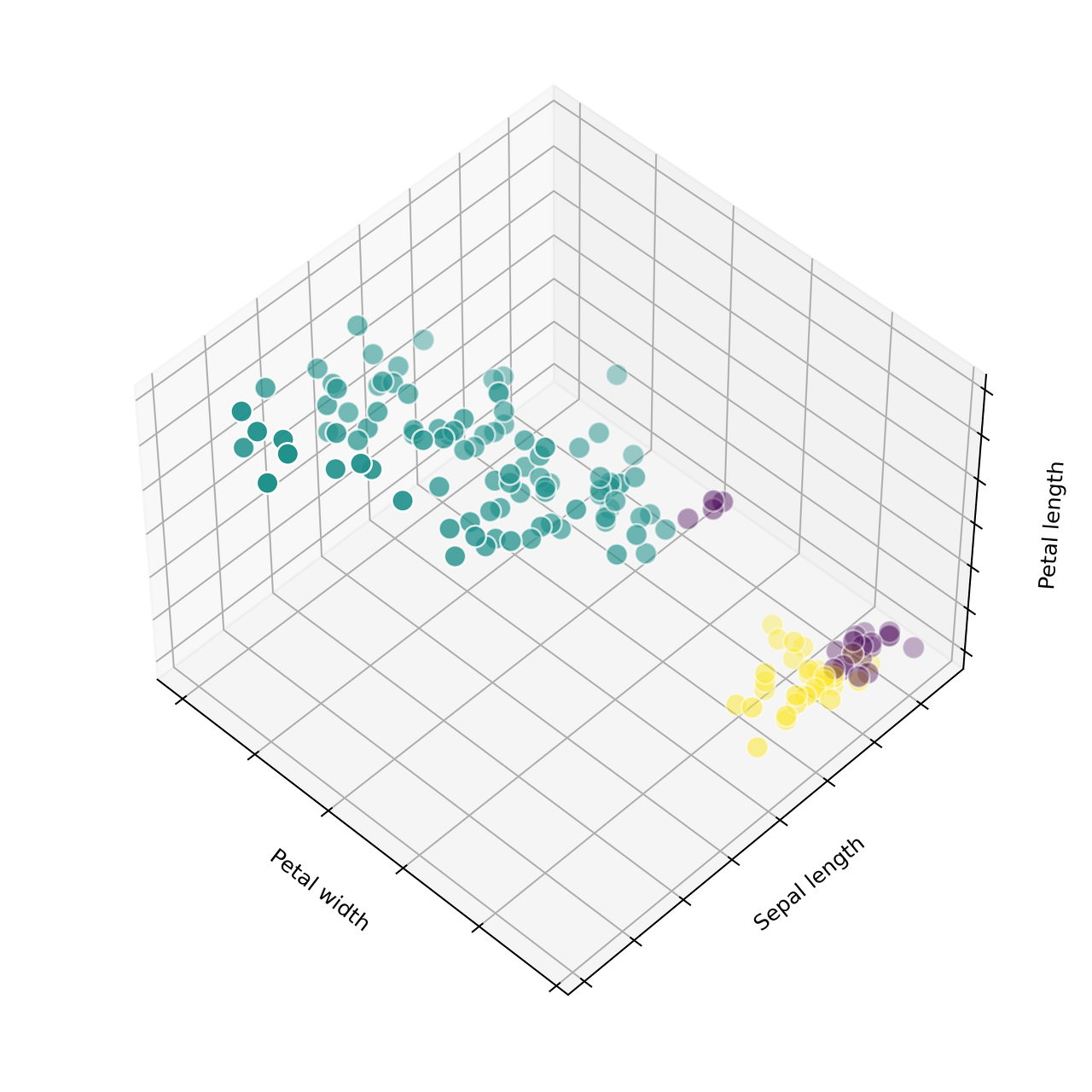kmeans-1kmeans-2kmeans-3
  • 1번 모델은 8개의 클러스터로 나눈 모델 (불필요하게 세분화시킴)
  • 3번 모델은 초기 중앙값을 랜덤으로 잡아서 특정 클러스터에 데이터가 몰림

Ground Truth (원본)

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12

fig = plt.figure(figsize=(7, 7))
ax = Axes3D(fig,  elev=48, azim=134)

for name, label in [('Setosa', 0), ('Versicolour', 1), ('Virginica', 2)]:
    ax.text3D(X[y == label, 3].mean(), X[y == label, 0].mean(), X[y == label, 2].mean()+2, 
              name, horizontalalignment='center')

ax.scatter(X[:, 3], X[:, 0], X[:, 2], c=y, edgecolor='w', s=100)

...

plt.show()

4. 최적의 클러스터 개수

최적의 클러스터 기준

  1. 같은 클러스터에 있는 데이터끼리 뭉쳐 있음
  2. 서로 다른 클러스터에 있는 데이터끼리 멀리 떨어져 있음

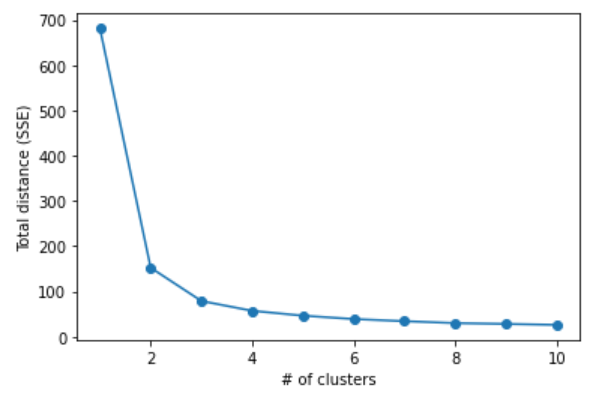
Elbow 기법

  • SSE(Sum of Squared Errors)의 값이 점점 줄어들다가 어느 순간
    줄어드는 비율이 급격하게 작아지는 부분이 발생
  • 결과물인 그래프 모양을 보면 팔꿈치에 해당하는 부분이 최적의 클러스터 개수가 됨
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14

def elbow(X):
    total_distance = []
    for i in range(1, 11):
        model = cluster.KMeans(n_clusters=i, random_state=0)
        model.fit(X)

        total_distance.append(model.inertia_) 

    plt.plot(range(1, 11), total_distance, marker='o')
    plt.xlabel('# of clusters')
    plt.ylabel('Total distance (SSE)')
    plt.show()

elbow(X)
  • model.inertia_: 샘플에 대해 가장 가까운 클러스터와의 거리 제곱의 합
  • inertia 값은 클러스터 수가 늘어날수록 감소
  • 같은 클러스터에 있는 데이터끼리 뭉쳐있는 정도만 확인 가능

elbow

Silhouette

  • 클러스터링의 품질을 정량적으로 계산해주는 방법 (모든 클러스터링 기법에 적용 가능)
  • i번째 데이터 x(i)에 대한 실루엣 계수 s(i) 값은 아래의 식으로 정의

silhouette

  • a(i): 클러스터 내 데이터 응집도(cohesion) 를 나타내는 값
    == 데이터 x(i)와 동일한 클러스터 내의 나머지 데이터들과의 평균 거리
  • b(i): 클러스터 간 분리도(separation) 를 나타내는 값
    == 데이터 x(i)와 가장 가까운 클러스터 내의 모든 데이터들과의 평균 거리
  • 클러스터의 개수가 최적화되어 있으면 실루엣 계수의 값은 1에 가까운 값이 됨
  • 실루엣 계수의 평균이 0.7 이상이면 안정적
1
2
3

from sklearn.metrics import silhouette_score

silhouette_avg = silhouette_score(X, y_fitted)
  • silhouette_avg: 실루엣 계수의 평균
  • 클러스터링의 기준이 이론적으로는 맞을 수 있어도 실용적으로는 다를 수 있음
    (판단 기준이 없을 때 활용)