Principal Component Analysis #

• 차원 축소를 통해 최소 차원의 정보로 원래 차원의 정보를 모사하는 알고리즘
• 데이터의 열의 수가 많아 학습 속도가 느려질 때 열의 수를 줄이기 위해 사용
• Dimension Reduction: 고차원 벡터에서 일부 차원의 값을 모두 0으로 만들어 차원을 줄임
• 원래의 고차원 벡터의 특성을 최대한 살리기 위해 가장 분산이 높은 방향으로 회전 변환 진행
• 전체 데이터를 기반으로 분산이 가장 큰 축을 찾아 PC 1으로 만들고,
  PC 1에 직교하는 축 중에서 분산이 가장 큰 축을 PC 2로 만드는 과정 반복
• 정보의 누락이 있기 때문에 경우에 따라 모델의 성능 하락 발생
• Feature Selection: 기존에 존재하는 열 중에 n개를 선택
• Feature Extraction: 기존에 있는 열들을 바탕으로 새로운 열들을 만들어냄 (차원 축소)

Learning Process #

Import Libraries #

from sklearn import decomposition
from sklearn import datasets

Load Model #

iris = datasets.load_iris()
x = iris.data
y = iris.target

Create Model #

model = decomposition.PCA(n_components=1) 

• component의 개수에 상관없이 PC 1은 언제나 동일

Model Fitting #

model.fit(x)
x1 = model.transform(x)

Plot Model #

Histogram (components=1) #

import seaborn as sns

sns.distplot(x1[y==0], color="b", bins=20, kde=False)
sns.distplot(x1[y==1], color="g", bins=20, kde=False)
sns.distplot(x1[y==2], color="r", bins=20, kde=False)

plt.xlim(-6, 6)

plt.show()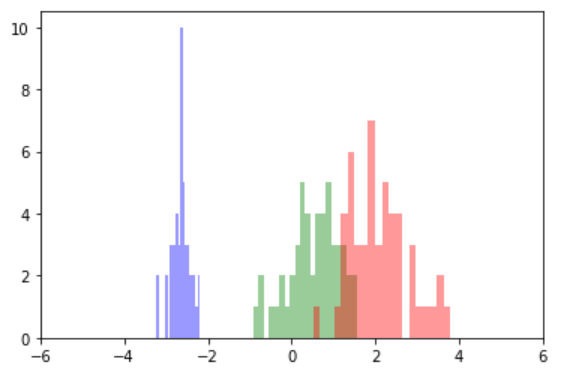

Scatter (components=3) #

plt.scatter(x[:, 0], x[:, 1], c=iris.target)
plt.xlabel('PC1')
plt.ylabel('PC2')
plt.show()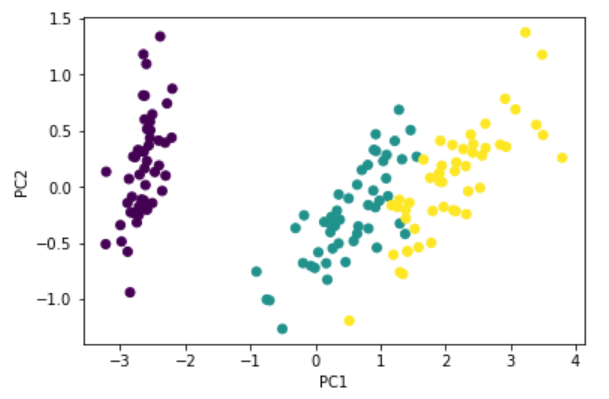

최적의 PCA 개수 #

데이터셋의 분산 정도 확인 #

• model.explained_variance_ratio_
• components가 전체 분산 정도 중 몇 퍼센트인지 확인
• 합쳐서 95퍼센트를 넘는 PCA 개수가 최적의 개수

최적의 PCA 개수 확인 #

np.argmax(np.cumsum(model.explained_variance_ratio_) >= 0.95 ) + 1

• np.cumsum: 값의 누적된 합계 계산
• np.argmax: 주어진 값들 중 가장 큰 값의 인덱스 번호

최적의 PCA 개수 적용 #

model = decomposition.PCA(n_components=0.95)
model.fit(x)
x = model.transform(x)